Congruence Modulo
Introduction To Congruence Modulo
You may see an expression like:
A≡B(mod C)
This says that A is congruent to B mod C.
We will discuss the meaning of congruence modulo by performing a thought experiment with the regular modulo operator.
Let's imagine we were calculating mod 5 for all of the integers:
Examples With Visualisation
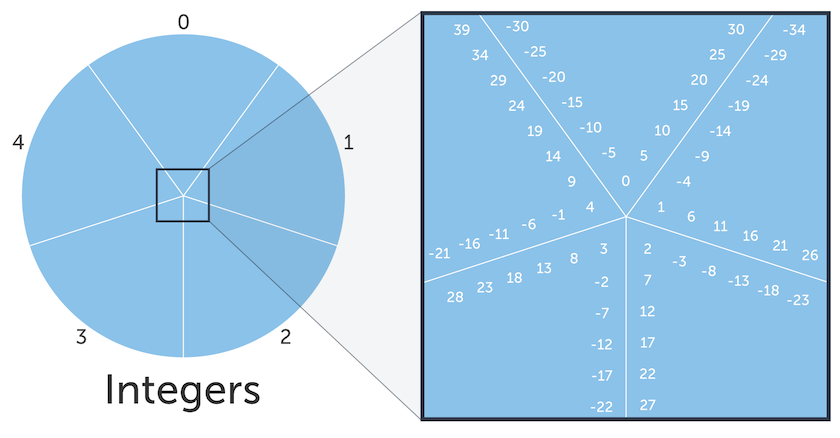
Suppose we labelled 5 slices 0, 1, 2, 3, 4.
Then, for each of the integers, we put it into a slice that matched the value of the integer mod 5. Think of these slices as buckets, which hold a set of numbers. For example, 26 would go in the slice labelled 1,
because 26 mod 5 = 1 Above is a figure that shows some integers that we would find in each of the slices.
It would be useful to have a way of expressing that numbers belonged in the same slice.
(Notice 26 is in the same slice as 1, 6, 11, 16, 21 in above example)
A common way of expressing that two values are in the same slice, is to say they are in the same equivalence class.
The way we express this mathematically for mod C is: A≡B (mod C)
In plain English, the above statement says "A is congruent to B modulo C."
Examining the expression closer:
1. ≡ is the symbol for congruence, which means the values A and B are in the same equivalence class.
2. The (mod C) within the parenthesis tells us what operation we applied to A and B.
3. When we have both of these, we call "≡" congruence modulo C.
Source : KhanAcademy.com
Congruency Tester
