Modular Arithmetic
An Introduction To Modular Math
Whe we divide two integers we get Equation :
A
-- = Q remainder R
B
Where :
A is Divident
B is Divisor
Q is Quotient
R is Remainder
Sometimes, we are only interested in finding the Remainder.
for these cases we use modulo operator (mod).
using abouve equation we have :
A mod B = R
Examples With Visualisation
8 mod 4 = ?
With a modulus of 4 we make a clock with numbers 0,1,2,3.
We start at 0 and go through 8 numbers in a clockwise sequence 1 -> 2 -> 3 -> 0 -> 1 -> 2 -> 3 -> 0.
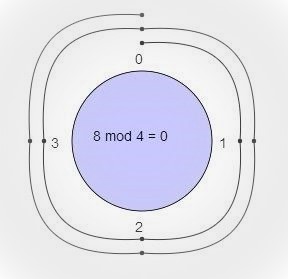
So, the Modulus will be 0.
7 mod 2 = ?
With a modulus of 2 we make a clock with numbers 0 and 1.
We start at 0 and go through 7 numbers in clockwise sequence 1 -> 0 -> 1 -> 0 -> 1 -> 0 -> 1.
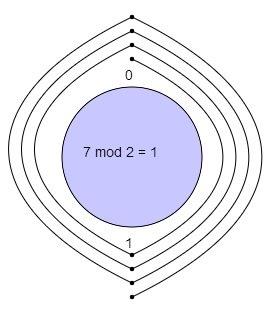
So the Modulus will be 1.
-5 mod 3 = ?
With a modulus of 3 we make a clock with numbers 0 , 1 and 2.
We start at 0 and go through 5 numbers in counter-clockwise sequence 2 -> 1 -> 0 -> 2 -> 1.
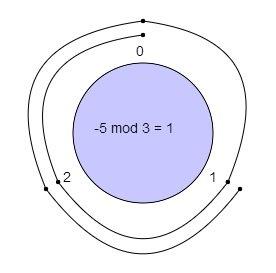
So the Modulus will be 1.
Source : KhanAcademy.com
Mod Evaluator
